College Algebra and Trigonometry form the foundation of higher mathematics, blending classical algebra with analytic geometry and introducing transcendental functions. These courses prepare students for precalculus and STEM fields, emphasizing problem-solving and critical thinking. Resources like free PDF textbooks and online guides are widely available, making learning accessible and efficient for students.
1.1 Importance of Algebra and Trigonometry in College Education
Algebra and trigonometry are fundamental in college education, serving as the cornerstone for STEM disciplines. They develop problem-solving skills, critical thinking, and mathematical reasoning. These subjects provide tools for analyzing real-world phenomena, making them essential for careers in physics, engineering, and data science. Mastery of algebra and trigonometry also prepares students for advanced courses like precalculus and calculus, ensuring a strong academic foundation.
1.2 Overview of the College Algebra and Trigonometry Curriculum
The curriculum covers foundational algebraic concepts, trigonometric functions, and their applications. It includes solving equations, graphing functions, and understanding exponential and logarithmic relationships. Students explore trigonometric identities, triangle solving, and analytic geometry. Practical problem-solving techniques are emphasized, preparing students for STEM fields and higher-level mathematics. The course structure ensures a balance between theoretical knowledge and real-world applications, fostering a comprehensive understanding of mathematical principles.
Scope and Sequence of College Algebra and Trigonometry
The curriculum is structured to progress from foundational algebraic concepts to advanced trigonometric functions, ensuring a logical flow that builds student proficiency for further mathematical studies.
2.1 Typical Chapters in a College Algebra Textbook
A typical college algebra textbook covers foundational topics such as algebraic simplification, functions, and graphs. Chapters often include polynomial and rational functions, exponential and logarithmic functions, and an introduction to trigonometry. Additional sections may explore conic sections and systems of equations, providing a comprehensive understanding of algebraic principles and their applications. The content is designed to build logical progression from basic to advanced mathematical concepts.
2.2 Key Topics in Trigonometry Covered in the Course
Trigonometry in the course covers essential topics such as trigonometric functions, solving triangles, and trigonometric identities. Students explore right and oblique triangles, learning to apply sine, cosine, and tangent functions. The curriculum also introduces exponential functions and logarithms, which are crucial for advanced problem-solving. These topics are designed to build a strong foundation for precalculus and calculus, ensuring a smooth transition to higher-level mathematics.
Key Concepts in College Algebra
College Algebra focuses on equations, inequalities, and functions, including polynomial and rational functions; These concepts build a foundation for advanced mathematics and problem-solving skills.
3.1 Equations, Inequalities, and Functions
College Algebra emphasizes solving linear, quadratic, and polynomial equations, as well as inequalities. Students learn to manipulate and simplify expressions, understanding function properties, including exponential and logarithmic functions. These concepts are essential for graphing and analyzing real-world problems, forming a strong foundation for advanced mathematics and STEM applications.
3.2 Graphs and Their Interpretations
Graphs play a crucial role in understanding function behavior and relationships in college algebra. Students learn to sketch and interpret graphs of polynomial, rational, and exponential functions. Key concepts include identifying intercepts, asymptotes, and intervals of increase or decrease. Graphical analysis helps in solving equations, inequalities, and real-world problems, providing visual insights into mathematical relationships and trends, which is essential for advanced problem-solving in STEM fields.
3.3 Polynomial and Rational Functions
Polynomial functions are fundamental in college algebra, with degrees dictating end behavior and turning points. Rational functions, defined as ratios of polynomials, introduce concepts like asymptotes and holes. Understanding these functions involves graphing, identifying key features, and solving equations. They are essential for modeling real-world phenomena, such as population growth and electrical circuits, making them vital tools in STEM problem-solving and analysis.

Trigonometric Functions and Identities
Trigonometric functions, including sine, cosine, and tangent, are essential for solving problems involving angles and triangles. They form the basis for trigonometric identities, simplifying complex equations in various STEM applications.
4.1 Definition and Properties of Trigonometric Functions
Trigonometric functions like sine, cosine, and tangent are defined as ratios of sides in a right triangle. They describe relationships between angles and side lengths, with properties including periodicity, even-odd characteristics, and co-function identities. These functions are fundamental for solving equations and modeling periodic phenomena, making them essential tools in STEM fields and various applications.
4.2 Trigonometric Identities and Their Applications
Trigonometric identities, such as the Pythagorean identity and sum/difference formulas, are essential for simplifying expressions and solving equations. These identities are widely applied in physics, engineering, and astronomy for modeling periodic phenomena and analyzing waves. They also facilitate the simplification of complex trigonometric expressions, making them indispensable tools in both academic and real-world problem-solving scenarios.
Applications of Algebra and Trigonometry
Algebra and trigonometry are vital in physics, engineering, and computer science, enabling problem-solving and modeling real-world phenomena. Their applications drive innovations in technology and data analysis.
5;1 Real-World Applications in Physics and Engineering
College algebra and trigonometry are essential tools in physics and engineering, enabling the solving of complex problems and modeling of real-world phenomena. Algebraic techniques are used to analyze wave functions, forces, and motion, while trigonometric identities simplify calculations in oscillatory systems and signal processing. Engineers rely on these mathematical foundations to design structures, optimize systems, and develop innovative technologies, making them indispensable in modern scientific advancements and practical applications.
5.2 Uses in Computer Science and Data Analysis
College algebra and trigonometry are fundamental in computer science and data analysis. Algebraic structures underpin algorithms and data analysis, while trigonometric functions are essential for signal processing and graphical representations. These mathematical tools enable advancements in artificial intelligence, game development, and machine learning, making them indispensable in modern computational fields and technological innovations.

Recommended Resources and Study Materials
Free PDF textbooks like Stitz-Zeager’s Precalculus and OpenStax’s College Algebra and Trigonometry are excellent resources. Online supplements and study guides provide additional practice problems and explanations.
6.1 Popular Textbooks and PDF Resources
Popular textbooks include Stitz-Zeager’s Precalculus and OpenStax’s College Algebra and Trigonometry, both available as free PDFs. Leithold’s College Algebra and Trigonometry and Simmons’ Precalculus Mathematics in a Nutshell are also widely used. These resources provide comprehensive coverage of algebra and trigonometry, with clear explanations and practice problems. They are accessible online, making them ideal for students seeking affordable and high-quality study materials;
6.2 Online Study Guides and Supplements
Online platforms like OpenStax and Khan Academy offer free study guides for college algebra and trigonometry. Websites such as stitz-zeager.com provide supplementary PDF chapters and practice problems. Additionally, tools like Desmos and GeoGebra enable interactive graphing and visualization. These resources complement textbooks, offering video tutorials, interactive exercises, and step-by-step solutions to enhance understanding and mastery of key concepts in algebra and trigonometry.
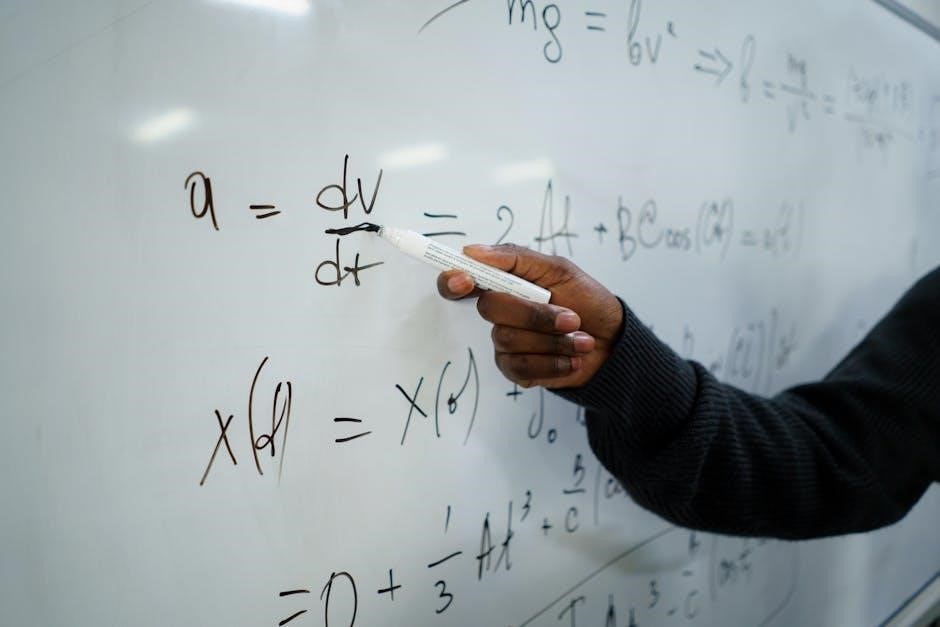
Practice Problems and Exercises
Practice problems in college algebra and trigonometry PDFs cover equations, inequalities, and trigonometric identities. Regular exercises help master concepts like solving quadratic equations and graphing functions effectively.
7.1 Types of Problems and Their Solutions
College algebra and trigonometry PDFs feature various problem types, including quadratic equations, trigonometric identities, and exponential functions. Solutions often involve step-by-step methods, such as factoring, graphing, or applying identities. Word problems require translating real-world scenarios into mathematical expressions. Regular practice with these exercises helps students master problem-solving strategies and conceptual understanding, ensuring readiness for advanced mathematics.
7.2 Importance of Regular Practice
Regular practice is essential for mastering college algebra and trigonometry; It reinforces problem-solving skills, improves conceptual understanding, and builds confidence. Consistent practice helps students identify weaknesses and develop strategies to overcome them. By solving various problem types, students prepare for exams and advanced courses. Utilizing PDF resources and online guides ensures access to exercises that enhance proficiency and retention of key mathematical concepts.

Test Preparation and Exam Strategies
Effective test preparation involves understanding question types, practicing past papers, and mastering problem-solving techniques. Utilize study guides and resources like cheat sheets for quick reference. Staying calm and managing time wisely during exams enhances performance and confidence.
8.1 Strategies for Effective Test Preparation
Effective test preparation for college algebra and trigonometry involves consistent practice and strategic review. Start by identifying weak areas and focus on improving them. Utilize free PDF resources, such as OpenStax textbooks, to access practice problems and study guides. Create a structured study schedule, dedicating time to reviewing key concepts and solving past exam questions. Regularly test yourself with timed practice exams to build time management skills and reduce exam anxiety. Seek clarification on complex topics from instructors or online forums to ensure a solid understanding. Finally, ensure adequate rest and a clear mind before the exam to perform at your best.
8.2 Tips for Solving Different Question Types
Mastering different question types in college algebra and trigonometry requires targeted strategies. For multiple-choice questions, eliminate incorrect answers first. Free-response questions demand clear step-by-step solutions; Word problems require translating descriptions into mathematical expressions. Practice identifying question patterns in PDF resources and past exams. Regularly review formulas and key concepts to build confidence in tackling various problem formats effectively.

The Role of Algebra in STEM Fields
Algebra is fundamental to STEM disciplines, providing essential tools for problem-solving and critical thinking. It underpins engineering, physics, and computer science, enabling the analysis of complex systems and data. Mastery of algebraic concepts ensures a strong foundation for advanced scientific and technological studies.
9.1 Algebra as a Foundation for STEM Disciplines
Algebra serves as the cornerstone for STEM fields, providing essential tools for problem-solving and analytical thinking. It enables the manipulation of mathematical models, crucial in engineering, physics, and computer science. By mastering algebraic principles, students gain the ability to interpret and transform complex systems, making it indispensable for advancing in science, technology, engineering, and mathematics.
9.2 Interconnections with Other STEM Subjects
Algebra is deeply intertwined with other STEM disciplines, such as physics, engineering, and computer science. It provides the mathematical framework for solving equations, modeling systems, and analyzing data. In physics, algebraic methods are used to describe motion and forces. In engineering, it aids in designing structures and optimizing processes. Similarly, computer science relies on algebra for algorithm development and data analysis, showcasing its versatility and indispensability across STEM fields.
Graphing Calculators in College Algebra and Trigonometry
Graphing calculators are essential tools for visualizing functions, solving equations, and exploring trigonometric identities. They enable students to analyze complex relationships and interpret mathematical concepts graphically.
10.1 Role of Graphing Calculators in Problem Solving
Graphing calculators play a pivotal role in solving algebraic and trigonometric problems by visualizing functions, inequalities, and identities. They enable students to explore mathematical relationships dynamically, fostering deeper understanding. These tools are particularly useful for analyzing complex equations, plotting graphs, and identifying key features like intercepts and asymptotes. Their versatility supports STEM fields by allowing users to model real-world phenomena and interpret data graphically, making them indispensable for modern problem-solving.
10.2 How to Use Them Effectively
To use graphing calculators effectively, familiarize yourself with their interface and functions. Start by entering equations accurately to avoid errors. Utilize the graphing mode to visualize functions and identify key features like maxima, minima, and intercepts. Explore built-in tools for solving equations and analyzing trigonometric identities. Regular practice with these devices enhances problem-solving skills and prepares students for advanced STEM applications, making them an essential tool in college algebra and trigonometry.
Common Challenges and Solutions
Students often struggle with algebraic expressions and trigonometric identities. Utilizing free PDF resources like OpenStax and practice guides can help overcome these challenges effectively and efficiently.
11.1 Overcoming Difficulties in Algebra
Common challenges in algebra include simplifying expressions, solving equations, and understanding functions. Free PDF resources like OpenStax’s College Algebra and Trigonometry provide detailed explanations and examples. Practice guides and online supplements offer step-by-step solutions, helping students grasp complex concepts. Regular practice and leveraging digital tools, such as graphing calculators, can significantly improve problem-solving skills and confidence in algebraic manipulation.
11.2 Strategies for Mastering Trigonometry
Mastering trigonometry requires understanding foundational concepts like trigonometric identities and right triangle definitions. Regular practice with problem sets from resources like College Algebra and Trigonometry PDFs is essential. Focus on applying identities to simplify and solve problems. Utilize online platforms and graphing calculators to visualize functions and enhance understanding. Breaking down complex problems into manageable steps and seeking supplementary guides can significantly improve proficiency in trigonometric analysis and applications.
Evolution of Teaching Methods
The integration of digital resources, such as free College Algebra and Trigonometry PDFs, has transformed teaching methods, offering flexible and accessible learning opportunities for students worldwide.
12.1 Impact of Digital Resources on Learning
Digital resources, such as free PDF textbooks, have revolutionized learning in college algebra and trigonometry. These materials provide flexible access to content, enabling self-paced study and enhanced engagement. OpenStax and other platforms offer peer-reviewed, openly licensed textbooks, reducing costs and ensuring quality education. Interactive tools and online supplements further enrich the learning experience, making complex concepts more approachable for students.
12.2 Benefits of Using PDF Textbooks
PDF textbooks offer numerous benefits, including free access to high-quality materials, offline usability, and easy sharing. They provide flexibility for students to study anywhere, reducing reliance on physical copies. Institutions can customize content to meet specific curriculum needs, ensuring relevance. Additionally, PDFs are environmentally friendly and cost-effective, making education more accessible and sustainable for a wider audience.
Interconnections Between Algebra and Trigonometry
Algebra provides the structural framework for solving trigonometric problems, enabling the manipulation of equations and identities. Together, they form a cohesive system for analyzing mathematical relationships and functions.
13.1 How Algebra Supports Trigonometric Problem Solving
Algebraic techniques are fundamental in solving trigonometric problems, providing tools to manipulate equations, functions, and identities. These methods enable simplification of expressions, solving for unknowns, and analyzing periodicity. For instance, solving trigonometric equations often relies on algebraic strategies to isolate variables. This integration enhances problem-solving efficiency and deepens understanding of mathematical relationships, making algebra indispensable in trigonometric analysis and applications.
13.2 Integrated Approach in Learning
An integrated approach combines college algebra and trigonometry, fostering a cohesive understanding of mathematical concepts. This method highlights connections between algebraic techniques and trigonometric functions, enhancing problem-solving skills. Resources like PDF textbooks and online guides support this unified learning strategy, allowing students to explore topics seamlessly. This approach not only simplifies complex ideas but also strengthens foundational knowledge, preparing students for advanced mathematical studies and real-world applications.
Career Relevance of Algebra and Trigonometry
Algebra and trigonometry are essential for careers in STEM fields, developing problem-solving and analytical skills. They are fundamental for physics, engineering, and data analysis, opening diverse career opportunities.
14.1 Career Opportunities in Mathematics and Related Fields
Mastering college algebra and trigonometry opens doors to lucrative careers in mathematics, engineering, physics, and computer science. These skills are essential for roles like data analysts, engineers, and researchers. Industries such as technology, finance, and healthcare also rely on strong algebraic and trigonometric foundations. With free PDF resources like OpenStax, students can access high-quality materials to prepare for these in-demand careers.
14.2 Skills Developed Through These Courses
College algebra and trigonometry cultivate problem-solving, critical thinking, and analytical reasoning. Students develop proficiency in mathematical modeling, data analysis, and logical reasoning. These courses enhance understanding of functions, graphs, and trigonometric identities, equipping students with skills vital for STEM fields, economics, and computer science. Mastery of these concepts also improves the ability to interpret and apply mathematical principles in real-world scenarios, supported by resources like PDF textbooks.

Tools and Software for Learning
Utilize mathematical software and online platforms like OpenStax and Stitz-Zeager for interactive learning. These tools offer free PDF textbooks and supplementary resources to enhance understanding and problem-solving skills.
15.1 Mathematical Software and Apps
Mathematical software like OpenStax and Stitz-Zeager offer interactive tools for college algebra and trigonometry. These platforms provide step-by-step solutions, interactive simulations, and downloadable PDF resources to aid in understanding complex concepts. Additionally, apps such as Photomath and Desmos are highly recommended for solving equations, graphing functions, and visualizing trigonometric identities, making learning more engaging and accessible for students at all levels.
15;2 Online Platforms for Supplementary Learning
Online platforms like Khan Academy, Coursera, and Udemy offer supplementary courses and resources for college algebra and trigonometry. Websites such as OpenStax and Stitz-Zeager provide free PDF textbooks and interactive tools. These platforms include video tutorials, practice exercises, and quizzes to reinforce learning. They cater to diverse learning styles, ensuring students can access additional support and resources to enhance their understanding of algebraic and trigonometric concepts effectively.
Mastering College Algebra and Trigonometry is essential for future STEM opportunities, providing foundational skills and problem-solving abilities. Utilize available PDF resources and online tools to enhance learning and prepare for advanced studies and diverse career paths.
16.1 Summary of Key Concepts
College Algebra and Trigonometry cover essential topics like equations, functions, graphs, polynomials, and rational functions. Trigonometry includes identities, triangle solving, and periodic functions. These courses emphasize problem-solving and critical thinking, preparing students for STEM fields and advanced mathematics. Resources like PDF textbooks and online guides provide comprehensive support for mastering these foundational concepts.
16.2 Encouragement for Further Study
Mastering college algebra and trigonometry unlocks opportunities in STEM fields and advanced mathematics. These foundational skills are essential for problem-solving and critical thinking. With free resources like OpenStax and Stitz-Zeager PDFs, students can continue exploring topics like calculus and precalculus. Encourage further study to deepen mathematical understanding and open doors to exciting career possibilities in engineering, physics, and computer science.